3.1 Aritmética de punto fijo
Un entero se puede representar empleando todos los bits de una palabra de computadora, con la salvedad de que se debe reservar un bit para el signo. Por ejemplo, en una máquina con longitud de palabra de 32 bits, los enteros están comprendidos entre -(231 - 1) y 231 - 1 = 2147483647. Un número representado en formato entero es 'exacto'. Las operaciones aritméticas entre números enteros son también 'exactas' siempre y cuando:- 1.
- La solución no esté fuera del rango del número entero más grande o más pequeño que se puede representar (generalmente con signo). En estos casos se dice que se comete un error de desbordamiento por exceso o por defecto (en inglés: Overflow y Underflow) y es necesario recurrir a técnicas de escalado para llevar a cabo las operaciones.
- 2.
- La división se interpreta que da lugar a un número entero, despreciando cualquier resto.
3.2 Números en punto flotante
3.2.1 Notación científica normalizada
En el sistema decimal, cualquier número real puede expresarse mediante la denominada notación científica normalizada. Para expresar un número en notación científica normalizada multiplicamos o dividimos por 10 tantas veces como sea necesario para que todos los dígitos aparezcan a la derecha del punto decimal y de modo que el primer dígito después del punto no sea cero. Por ejemplo: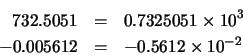
En general, un número real x distinto de cero, se representa en notación científica normalizada en la forma:
en donde r es un número tal que
donde m es un entero. El número q se denomina mantisa y el entero m exponente. En un ordenador binario tanto q como m estarán representados como números en base 2. Puesto que la mantisa q está normalizada, en la representación binaria empleada se cumplirá que:
3.2.2 Representación de los números en punto flotante
En un ordenador típico los números en punto flotante se representan de la manera descrita en el apartado anterior, pero con ciertas restricciones sobre el número de dígitos de q y m impuestas por la longitud de palabra disponible (es decir, el número de bits que se van a emplear para almacenar un número). Para ilustrar este punto, consideraremos un ordenador hipotético que denominaremos MARC-32 y que dispone de una longitud de palabra de 32 bits (muy similar a la de muchos ordenadores actuales). Para representar un número en punto flotante en el MARC-32, los bits se acomodan del siguiente modo:| Signo del número real x: | 1 bit |
| Signo del exponente m: | 1 bit |
| Exponente (entero |m|): | 7 bits |
| Mantisa (número real |q|): | 23 bits |
Se dice que un número real expresado como aparece en la ecuación (18) y que satisface la ecuación (19) tiene la forma de punto flotante normalizado. Si además puede representarse exactamente con |m| ocupando 7 bits y |q| ocupando 24 bits, entonces es un número de máquina en el MARC-323
La restricción de que |m| no requiera más de 7 bits significa que:
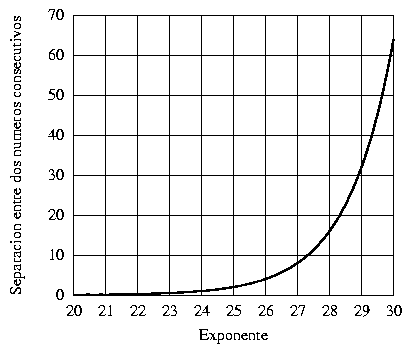
Como q debe representarse empleando no más de 24 bits significa que nuestros números de máquina tienen una precisión limitada cercana a las siete cifras decimales, ya que el bit menos significativo de la mantisa representa unidades de
Por ejemplo: 0.5 representado en punto flotante en el MARC-32 (longitud de palabra de 32 bits) se almacena en la memoria del siguiente modo:
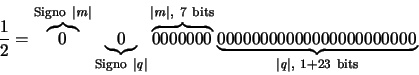
Solución: El número 26.32 en binario se escribe del siguiente modo:
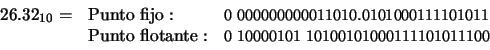
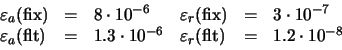
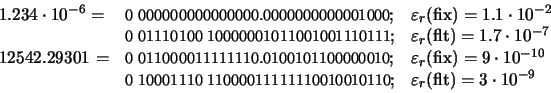
3.3 Aritmética de punto flotante
En este apartado analizaremos los errores inherentes a la aritmética de los números de punto flotante. Primero consideraremos el error que surge como consecuencia de que los números reales no se pueden almacenar, en general, de forma exacta en un ordenador. Después analizaremos las cuatro operaciones aritméticas básicas y finalmente ampliaremos el estudio a un cálculo más complejo.3.3.1 Números de máquina aproximados
Estamos interesados en estimar el error en que se incurre al aproximar un número real positivo x mediante un número de máquina del MARC-32. Si representamos el número mediante:en donde cada ai es 0 ó 1 y el bit principal es a1 = 1. Un número de máquina se puede obtener de dos formas:
- Truncamiento: descartando todos los bits excedentes
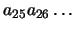 . El número resultante, x' es siempre menor que x (se encuentra a la izquierda de x en la recta real).
. El número resultante, x' es siempre menor que x (se encuentra a la izquierda de x en la recta real). - Redondeo por exceso: Aumentamos en una unidad el último bit remanente a24 y después eliminamos el exceso de bits como en el caso anterior.
que se puede escribir de la siguiente forma:
Ejemplo 6: ¿Cómo se expresa en binario el número x = 2/3? ¿Cuáles son los números de máquina x' y x'' próximos en el MARC-32? El número 2/3 en binario se expresa como:
Los dos números de máquina próximos, cada uno con 24 bits, son:
| x' | = | ||
| x'' | = |
en donde x' se ha obtenido por truncamiento y x'' mediante redondeo por exceso. Calculamos ahora las diferencias x - x' y x'' - x para estimar cual es el error cometido:
| x - x' | = | 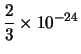 | |
| x'' - x | = | 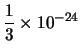 |
Por tanto, el número más próximo es fl(x) = x'' y los errores de redondeo absoluto y relativo son:
| |fl(x) - x| | = | 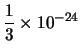 | |
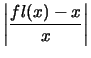 | = | 2-25 < 2-24 |
3.3.2 Las operaciones básicas
Vamos a analizar el resultado de operar sobre dos números en punto flotante normalizado de l-dígitos de longitud, x e y, que producen un resultado normalizado de l-dígitos. Expresaremos esta operación como:en donde op es +, -,
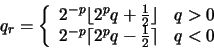
en donde la función redondeo por defecto
y un error relativo máximo en el intervalo:
Analizaremos ahora el error generado por cada una de las operaciones básicas:
- Multiplicación.
- La operación de multiplicar dos números expresados en punto flotante implica sumar los exponentes y multiplicar las mantisas. Si la mantisa resultante no está normalizada, se recurre a renormalizar el resultado ajustando adecuadamente el exponente. Después, es necesario redondear la mantisa a p bits. Para analizar el error de esta operación supongamos dos números:
Tenemos entonces que el producto será:
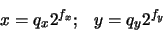 xy = qx qy 2fx + fyen donde el valor de la mantisa se encontrará en el rango:ya que tanto x como y satisfacen la ecuación (19). Por tanto, la normalización del producto qx qy implica un desplazamiento a la derecha de, como máximo, una posición. La mantisa redondeada será entonces uno de estos dos posibles valores:
xy = qx qy 2fx + fyen donde el valor de la mantisa se encontrará en el rango:ya que tanto x como y satisfacen la ecuación (19). Por tanto, la normalización del producto qx qy implica un desplazamiento a la derecha de, como máximo, una posición. La mantisa redondeada será entonces uno de estos dos posibles valores: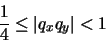 en donde
en donde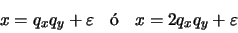
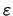 , que es el error de redondeo, cumple la ecuación (21). Tenemos entonces:
en donde, de acuerdo con la ecuación (22), tenemos:
, que es el error de redondeo, cumple la ecuación (21). Tenemos entonces:
en donde, de acuerdo con la ecuación (22), tenemos: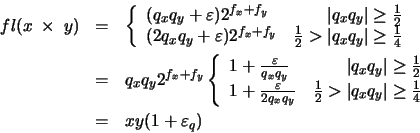 Por tanto, la cota del error relativo en la multiplicación es la misma que la que surge por redondear la mantisa.
Por tanto, la cota del error relativo en la multiplicación es la misma que la que surge por redondear la mantisa.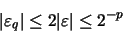
- División.
- Para llevar a cabo la división en punto flotante, se divide la mitad de la mantisa del numerador por la mantisa del denominador (para evitar cocientes mayores de la unidad), mientras que los exponentes se restan. Esto es:
Puesto que ambas mantisas satisfacen la ecuación (18), el valor del cociente estará acotado entre los límites:
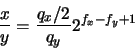 Aplicando un análisis similar al empleado en el caso de la multiplicación, obtenemos:
Aplicando un análisis similar al empleado en el caso de la multiplicación, obtenemos: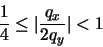 en donde, de acuerdo con la ecuación (22), tenemos:
en donde, de acuerdo con la ecuación (22), tenemos: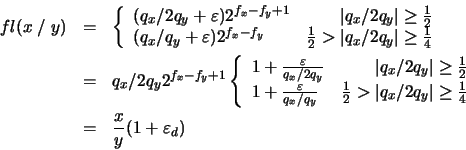 Es decir, la cota máxima del error relativo en la división, como en el caso anterior, es la misma que la que surge por redondear la mantisa.
Es decir, la cota máxima del error relativo en la división, como en el caso anterior, es la misma que la que surge por redondear la mantisa.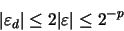
- Adición y sustracción.
- La operación de suma o resta se realiza del siguiente modo: se toma la mantisa del operando de menor magnitud (supongamos que es y) y se desplaza fx - fy posiciones a la derecha. La mantisa resultante es sumada (o restada) y el resultado se normaliza y después se redondea. Es decir:
El análisis del error cometido en esta operación es más complejo que los estudiados hasta ahora, por lo que no lo vamos a ver en detalle. Sin embargo, el resultado final indica que la cota máxima del error cometido en la adición y la sustracción viene dado por:
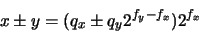
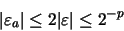
Sin embargo, los errores de redondeo se acumulan a medida que aumenta el número de cálculos. Si en el proceso de calcular un valor se llevan a cabo N operaciones aritméticas es posible obtener, en el mejor de los casos, un error de redondeo total del orden de
- Es muy frecuente que la regularidad del cálculo o las peculiaridades del computador den lugar a que el error se acumule preferentemente en una dirección; en cuyo caso el error de redondeo se puede aproximar a
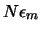 .
. - En circunstancias especialmente desfavorables pueden existir operaciones que incremente espectacularmente el error de redondeo. Generalmente, este fenómeno se da cuando se calcula la diferencia entre dos números muy próximos, dando lugar a un resultado en el cual los únicos bits significativos que no se cancelan son los de menor orden (en los únicos en que difieren). Puede parecer que la probabilidad de que se de dicha situación es pequeña, sin embargo, algunas expresiones matemáticas fomentan este fenómeno.
ax2 + bx + c = 0
que son:
Cualquiera de estas dos expresiones da problemas cuando a, c o ambos, son pequeños. En estos casos, el valor del discriminante es muy próximo al valor de b:
por lo que la diferencia
y las dos raíces a partir de valor de q como:
Ejemplo: Calcular las raíces de la siguiente ecuación cuadrática:
ax2 + bx + c = 0
siendo:
Solución: Empleando la ecuación (23), obtenemos:
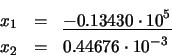
Sin embargo, empleando la expresión (24):
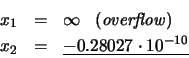
Por último, empleando las expresiones (25) y (26) se obtienen ambas soluciones correctas:
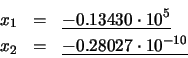
3.4 Desbordamiento por exceso y desbordamiento por defecto
En la discusión anterior, hemos ignorado la posibilidad de que el resultado de una operación del punto flotante pueda no ser representable mediante el esquema fijo (l-bits) empleado por el ordenador. La magnitud más grande que puede representarse mediante la fórmula general (18) es:en donde F es el mayor exponente positivo representable (generalmente 27 - 1) y M es la mantisa que tiene todos sus bits puestos a 1 ( M = 1 - 224). Un desbordamiento por exceso de punto flotante (overflow en inglés) se origina cuando el resultado de una operación de punto flotante tiene una magnitud mayor que la representada por la ecuación (27). Ejemplo: Con q = 8 (y por tanto F = 27 - 1 = 127), las siguientes operaciones aritméticas dan lugar a desbordamiento por exceso:
El desbordamiento por defecto (underflow en inglés) se produce cuando el resultado de una operación en punto flotante es demasiado pequeño, aunque no nulo, como para que se pueda expresar en la forma dada por la ecuación (18). El número más pequeño representable suponiendo que siempre trabajamos con mantisas normalizadas es
Ejemplo: Con q = 8 (y por tanto -F = -128), la siguiente operación aritmética da lugar a desbordamiento por defecto:
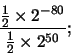
El desbordamiento por exceso es casi siempre resultado de un error en el cálculo. Sin embargo, en el caso del desobordamiento por defecto, en muchas ocasiones es posible continuar el cálculo reemplazando el resultado por cero.
3.5 Condicionamiento y estabilidad
La 'inestabilidad' en un cálculo es un fenómeno que se produce cuando los errores de redondeo individuales se propagan a través del cálculo incrementalmente. Veamos brevemente este fenómeno y el problema relacionado con este: el 'condicionamiento' del método o del problema. La mejor forma de ver este fenómeno es a través de un ejemplo. Supongamos el siguiente sistema de ecuaciones diferenciales: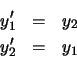
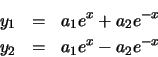
Hasta este punto, las soluciones son exactas. Sin embargo, supongamos que el sistema de ecuaciones anterior se resuelve empleando un método numérico cualquiera con el fin de calcular los valores de las funciones y1 y y2 en una secuencia de puntos
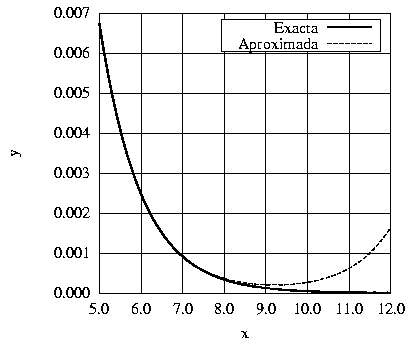
Representación de Números
Representación Numérica en una base
Dado un númerodonde el signo  es igual a 0 o 1 y los coeficientes
es igual a 0 o 1 y los coeficientes  son enteros positivos menores que
son enteros positivos menores que  . En la vida real la suma tiene sólo un número finito de términos por lo que algunos números son sólo representados en forma aproximada. Usualmente, utilizamos el sistema decimal de numeración (
. En la vida real la suma tiene sólo un número finito de términos por lo que algunos números son sólo representados en forma aproximada. Usualmente, utilizamos el sistema decimal de numeración ( ) pero la representación numérica en sistemas digitales se realiza en general en base 2, denominado sistema de numeración binaria, y ocasionalmente en base 16 (sistema hexadecimal). Los números se representan en memoria como una cadena de bits que pueden tomar los valores 0 ó 1. Se denomina byte a un grupo de 8 bits consecutivos.
) pero la representación numérica en sistemas digitales se realiza en general en base 2, denominado sistema de numeración binaria, y ocasionalmente en base 16 (sistema hexadecimal). Los números se representan en memoria como una cadena de bits que pueden tomar los valores 0 ó 1. Se denomina byte a un grupo de 8 bits consecutivos.
Representación de números enteros
En representación binaria un número entero donde cada coeficiente  es igual a 1 o 0. Usualmente los números enteros ocupaban 4 bytes de memoria (32 bits), aunque en las computadoras modernas se pueden utilizar enteros de 64 bits. Los números que pueden almacenarse en la representación de 4 bytes están en el rango:
es igual a 1 o 0. Usualmente los números enteros ocupaban 4 bytes de memoria (32 bits), aunque en las computadoras modernas se pueden utilizar enteros de 64 bits. Los números que pueden almacenarse en la representación de 4 bytes están en el rango:

para números enteros sin signo. Si se utiliza el primer bit de la izquierda como signo (0, positivo; 1, negativo) el rango se reduce a  y
y  para enteros con signo.
para enteros con signo.
Representación de números reales
Las computadoras, con un número finito de bits, no pueden almacenar todos los números reales en forma exacta. Esto es similar a lo que ocurre con los números irracionales (como
Algunos ejemplos
Para aclarar los conceptos, consideremos algunos ejemplos de números normalizados en precisión simple: - El signo es positivo (bit de signo igual a 0).
- El exponente se obtiene como
 , que en sistema decimal da
, que en sistema decimal da  .
. - La mantisa
 se obtiene sumando: 1 (implícito), 1/8, 1/16, 1/32, 1/64 y 1/1024.
se obtiene sumando: 1 (implícito), 1/8, 1/16, 1/32, 1/64 y 1/1024.
por lo que, después de eliminar la parte entera y agregando el signo y el exponente, el número es:
Aritmética con números binarios
Una de las consecuencias más importantes de usar una representación de punto flotante (con signo, mantisa y exponente) es que dos números deben tener el mismo exponente para poder ser sumados o restados. Consideremos por ejemplo la suma de los dos números anteriores
Casos particulares y otros ejemplos
- ¿Qué pasa cuándo el número es exactamente cero?.
La convención dice que se interpreta exactamente cero cuando todos los bits son 0. Esto significa, No sólo los de la mantisa sino también los del exponente. Nótese que para números de 64 bits (8 bytes) se interpreta que el número  , ya que el exponente ha sido corrido en 127.
, ya que el exponente ha sido corrido en 127.
- Representación de infinitos varios
Hay dos tipos de infinitos: positivos y negativos. La convención para representar estos números dice que un número se considera infinito si cada uno de los bits del exponente es 1 y los de la mantisa son 0. El signo permite distinguir entre  y
y  .
.
- Otro caso particular en la convención es cuando necesitamos representar algo que no corresponde a un número bien definido (
 , por ejemplo). El resultado de estas operaciones no son números (uno obtiene algo como
, por ejemplo). El resultado de estas operaciones no son números (uno obtiene algo como  NaN) y la representación interna corresponde a todos los bits del exponente en 1 y además al menos uno de la mantisa es 1 también.
NaN) y la representación interna corresponde a todos los bits del exponente en 1 y además al menos uno de la mantisa es 1 también.
Ejercicios
|
ARITMERTICA DE PUNTO FLKOTANTE
Problemas y Limitaciones
Los números de punto flotante se representan en el hardware de la computadora en fracciones en base 2 (binario). Por ejemplo, la fracción decimal0.1250.001Desafortunadamente, la mayoría de las fracciones decimales no pueden representarse exactamente como fracciones binarias. Como consecuencia, en general los números de punto flotante decimal que ingresás en la computadora son sólo aproximados por los números de punto flotante binario que realmente se guardan en la máquina.
El problema es más fácil de entender primero en base 10. Considerá la fracción 1/3. Podés aproximarla como una fracción de base 10
0.30.330.333De la misma manera, no importa cuantos dígitos en base 2 quieras usar, el valor decimal 0.1 no puede representarse exactamente como una fracción en base 2. En base 2, 1/10 es la siguiente fracción que se repite infinitamente:
0.0001100110011001100110011001100110011001100110011...>>> 0.1
0.10000000000000001>>> 0.1
0.10000000000000000555111512312578270211815834045410156250.10000000000000001Notá que esta es la verdadera naturaleza del punto flotante binario: no es un error de Python, y tampoco es un error en tu código. Verás lo mismo en todos los lenguajes que soportan la aritmética de punto flotante de tu hardware (a pesar de que en algunos lenguajes por omisión no muestren la diferencia, o no lo hagan en todos los modos de salida).
La función integrada :func: str de Python produce sólo 12 dígitos significativos, y quizás quieras usar esa. Normalmente eval(str(x)) no reproducirá x, pero la salida quizás sea más placentera de ver:
>>> print str(0.1)
0.1A esta se siguen otras sorpresas. Por ejemplo, luego de ver:
>>> 0.1
0.10000000000000001>>> round(0.1, 1)
0.10000000000000001Otra consecuencia es que como 0.1 no es exactamente 1/10, sumar diez valores de 0.1 quizás tampoco dé exactamente 1.0:
>>> suma = 0.0
>>> for i in range(10):
... suma += 0.1
...
>>> suma
0.9999999999999999Como dice cerca del final, “no hay respuestas fáciles”. A pesar de eso, ¡no le tengas mucho miedo al punto flotante! Los errores en las operaciones flotantes de Python se heredan del hardware de punto flotante, y en la mayoría de las máquinas están en el orden de no más de una 1 parte en 2**53 por operación. Eso es más que adecuado para la mayoría de las tareas, pero necesitás tener en cuenta que no es aritmética decimal, y que cada operación de punto flotante sufre un nuevo error de redondeo.
A pesar de que existen casos patológicos, para la mayoría de usos casuales de la aritmética de punto flotante al final verás el resultado que esperás si simplemente redondeás lo que mostrás de tus resultados finales al número de dígitos decimales que esperás. str() es normalmente suficiente, y para un control más fino mirá los parámetros del método de formateo str.format() en formatstrings.
14.1. Error de Representación¶
Esta sección explica el ejemplo “0.1” en detalle, y muestra como en la mayoría de los casos vos mismo podés realizar un análisis exacto como este. Se asume un conocimiento básico de la representación de punto flotante binario.Error de representación se refiere al hecho de que algunas (la mayoría) de las fracciones decimales no pueden representarse exactamente como fracciones binarias (en base 2). Esta es la razón principal de por qué Python (o Perl, C, C++, Java, Fortran, y tantos otros) frecuentemente no mostrarán el número decimal exacto que esperás:
>>> 0.1
0.100000000000000011 / 10 ~= J / (2**N)J ~= 2**N / 10>>> 2**52
4503599627370496L
>>> 2**53
9007199254740992L
>>> 2**56/10
7205759403792793L>>> q, r = divmod(2**56, 10)
>>> r
6L>>> q+1
7205759403792794L7205759403792794 / 72057594037927936Entonces la computadora nunca “ve” 1/10: lo que ve es la fracción exacta de arriba, la mejor aproximación al flotante doble de 754 que puede obtener:
>>> .1 * 2**56
7205759403792794.0>>> 7205759403792794 * 10**30 / 2**56
100000000000000005551115123125L
No hay comentarios:
Publicar un comentario